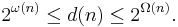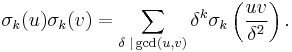Arithmetic function
In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers (i.e. positive integers) that "expresses some arithmetical property of n."[1]
An example of an arithmetic function is the non-principal character (mod 4) defined by
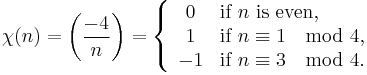 where
where  is the Kronecker symbol.
is the Kronecker symbol.
To emphasise that they are being thought of as functions rather than sequences, values of an arithmetic function are usually denoted by a(n) rather than an.
There is a larger class of number-theoretic functions that do not fit the above definition, e.g. the prime-counting functions. This article provides links to functions of both classes.
Notation
 and
and  mean that the sum or product is over all prime numbers:
mean that the sum or product is over all prime numbers:
Similarly,  and
and 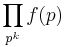 mean that the sum or product is over all prime powers with strictly positive exponent (so 1 is not counted):
mean that the sum or product is over all prime powers with strictly positive exponent (so 1 is not counted):
 and
and 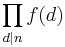 mean that the sum or product is over all positive divisors of n, including 1 and n. E.g., if n = 12,
mean that the sum or product is over all positive divisors of n, including 1 and n. E.g., if n = 12,
The notations can be combined:  and
and 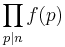 mean that the sum or product is over all prime divisors of n. E.g., if n = 18,
mean that the sum or product is over all prime divisors of n. E.g., if n = 18,
and similarly  and
and 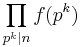 mean that the sum or product is over all prime powers dividing n. E.g., if n = 24,
mean that the sum or product is over all prime powers dividing n. E.g., if n = 24,
Multiplicative and additive functions
An arithmetic function a is
- completely additive if a(mn) = a(m) + a(n) for all natural numbers m and n;
- completely multiplicative if a(mn) = a(m)a(n) for all natural numbers m and n;
Two whole numbers m and n are called coprime if their greatest common divisor is 1; i.e., if there is no prime number that divides both of them.
Then an arithmetic function a is
- additive if a(mn) = a(m) + a(n) for all coprime natural numbers m and n;
- multiplicative if a(mn) = a(m)a(n) for all coprime natural numbers m and n.
Ω(n), ω(n), νp(n) - prime power decomposition
The fundamental theorem of arithmetic states that any positive integer n can be factorised uniquely as a product of powers of primes:  where p1 < p2 < ... < pk are primes and the aj are positive integers. (1 is given by the empty product.)
where p1 < p2 < ... < pk are primes and the aj are positive integers. (1 is given by the empty product.)
It is often convenient to write this as an infinite product over all the primes, where all but a finite number have a zero exponent. Define νp(n) as the exponent of the highest power of the prime p that divides n. I.e. if p is one of the pi then νp(n) = ai, otherwise it is zero. Then
In terms of the above the functions ω and Ω are defined by
- ω(n) = k,
- Ω(n) = a1 + a2 + ... + ak.
To avoid repetition, whenever possible formulas for the functions listed in this article are given in terms of n and the corresponding pi, ai, ω, and Ω.
Multiplicative functions
σk(n), τ(n), d(n) - divisor sums
σk(n) is the sum of the kth powers of the positive divisors of n, including 1 and n, where k is a complex number.
σ1(n), the sum of the (positive) divisors of n, is usually denoted by σ(n).
Since a positive number to the zero power is one, σ0(n) is therefore the number of (positive) divisors of n; it is usually denoted by d(n) or τ(n) (for the German Teiler = divisors).
Setting k = 0 in the second product gives
φ(n) - Euler totient function
φ(n), the Euler totient function, is the number of positive integers not greater than n that are coprime to n.
μ(n) - Möbius function
μ(n), the Möbius function, is important because of the Möbius inversion formula. See Dirichlet convolution, below.
This implies that μ(1) = 1. (Because Ω(1) = ω(1) = 0.)
τ(n) - Ramanujan tau function
τ(n), the Ramanujan tau function, is defined by its generating function identity:
Although it is hard to say exactly what "arithmetical property of n" it "expresses",[2] (τ(n) is (2π)−12 times the nth Fourier coefficient in the q-expansion of the modular discriminant function)[3] it is included among the arithmetical functions because it is multiplicative and it occurs in identities involving certain σk(n) and rk(n) functions (because these are also coefficients in the expansion of modular forms).
cq(n) - Ramanujan's sum
cq(n), Ramanujan's sum, is the sum of the nth powers of the primitive qth roots of unity:
Even though it is defined as a sum of complex numbers (irrational for most values of q), it is an integer. For a fixed value of n it is multiplicative in q:
- If q and r are coprime,
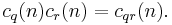
Many of the functions mentioned in this article have expansions as series involving these sums; see the article Ramanujan's sum for examples.
Completely multiplicative functions
λ(n) - Liouville function
λ(n), the Liouville function, is defined by
χ(n) - characters
All Dirichlet characters χ(n) are completely multiplicative; e.g. the non-principal character (mod 4) defined in the introduction, or the principal character (mod n) defined by
Additive functions
ω(n) - distinct prime divisors
ω(n), defined above as the number of distinct primes dividing n, is additive
Completely additive functions
Ω(n) - prime divisors
Ω(n), defined above as the number of prime factors of n counted with multiplicities, is completely additive.
νp(n) - prime power dividing n
For a fixed prime p, νp(n), defined above as the exponent of the largest power of p dividing n, is completely additive.
Neither multiplicative nor additive
π(x), Π(x), θ(x), ψ(x) - prime count functions
Unlike the other functions listed in this article, these are defined for non-negative real (not just integer) arguments. They are used in the statement and proof of the prime number theorem.
π(x), the prime counting function, is the number of primes not exceeding x.
A related function counts prime powers with weight 1 for primes, 1/2 for their squares, 1/3 for cubes, ...
θ(x) and ψ(x), the Chebyshev functions are defined as sums of the natural logarithms of the primes not exceeding x:
Λ(n) - von Mangoldt function
Λ(n), the von Mangoldt function, is 0 unless the argument is a prime power, in which case it is the natural log of the prime:
p(n) - partition function
p(n), the partition function, is the number of ways of representing n as a sum of positive integers, where two representations with the same summands in a different order are not counted as being different:
λ(n) - Carmichael function
λ(n), the Carmichael function, is the smallest positive number such that  for all a coprime to n. Equivalently, it is the least common multiple of the orders of the elements of the multiplicative group of integers modulo n.
for all a coprime to n. Equivalently, it is the least common multiple of the orders of the elements of the multiplicative group of integers modulo n.
For powers of odd primes and for 2 and 4, λ(n) is equal to the Euler totient function of n; for powers of 2 greater than 4 it is equal to one half of the Euler totient function of n:
and for general n it is the least common multiple of λ of each of the prime power factors of n:
h(n) - Class number
h(n), the class number function, is the order of the ideal class group of an algebraic extension of the rationals with discriminant n. The notation is ambiguous, as there are in general many extensions with the same discriminant. See quadratic field and cyclotomic field for classical examples.
rk(n) - Sum of k squares
rk(n) is the number of ways n can be represented as the sum of k squares, where representations that differ only in the order of the summands or in the signs of the square roots are counted as different.
Summation functions
Given an arithmetic function a(n), its summation function A(x) is defined by
A can be regarded as a function of a real variable. Given a positive integer m, A is constant along open intervals m < x < m + 1, and has a jump discontinuity at each integer for which a(m) ≠ 0.
Since such functions are often represented by series and integrals, to achieve pointwise convergence it is usual to define the value at the discontinuities as the average of the values to the left and right:
Individual values of arithmetic functions may fluctuate wildly - as in most of the above examples. Summation functions "smooth out" these fluctuations. In some cases it may be possible to find asymptotic behaviour for the summation function for large x.
A classical example of this phenomenon[4] is given by d(n), the number of divisors of n:
Dirichlet convolution
Given an arithmetic function a(n), let Fa(s), for complex s, be the function defined by the corresponding Dirichlet series (where it converges):[5]
Fa(s) is called a generating function of a(n). The simplest such series, corresponding to the constant function a(n) = 1 for all n, is ς(s) the Riemann zeta function.
The generating function of the Möbius function is the inverse of the zeta function:
Consider two arithmetic functions a and b and their respective generating functions Fa(s) and Fb(s). The product Fa(s)Fb(s) can be computed as follows:
It is a straightforward exercise to show that if c(n) is defined by
then
This function c is called the Dirichlet convolution of a and b, and is denoted by  .
.
A particularly important case is convolution with the constant function a(n) = 1 for all n, corresponding to multiplying the generating function by the zeta function:
Multiplying by the inverse of the zeta function gives the Möbius inversion formula:
If f is multiplicative, then so is g. If f is completely multiplicative, then g is multiplicative, but may or may not be completely multiplicative. The article multiplicative function has a short proof.
Relations among the functions
There are a great many formulas connecting arithmetical functions with each other and with the other functions of analysis - in fact, a large part of elementary and analytic number theory is a detailed study of these relations. See the articles on the individual functions for details.
Here are a few examples:
Dirichlet convolutions
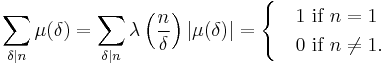 where λ is the Liouville function. [6]
where λ is the Liouville function. [6]
-
 Möbius inversion
Möbius inversion
-
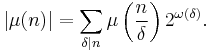 Möbius inversion
Möbius inversion
-
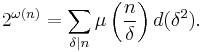 Möbius inversion
Möbius inversion
-
 Möbius inversion
Möbius inversion
 where λ is the Liouville function. [10]
where λ is the Liouville function. [10]
-
 Möbius inversion
Möbius inversion
Sums of squares
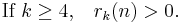 (Lagrange's four-square theorem).
(Lagrange's four-square theorem).
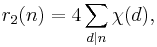 where χ is the non-principal character (mod 4) defined in the introduction.[12]
where χ is the non-principal character (mod 4) defined in the introduction.[12]
Define the function σk*(n) as[17]
That is, if n is odd, σk*(n) is the sum of the kth powers of the divisors of n, i.e. σk(n), and if n is even it is the sum of the kth powers of the even divisors of n minus the sum of the kth powers of the odd divisors of n.
Adopt the convention that Ramanujan's τ(x) = 0 if x is not an integer.
Divisor sum convolutions
Here "convolution" does not mean "Dirichlet convolution" but instead refers to the formula for the coefficients of the product of two power series:
The sequence 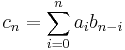 is called the convolution or the Cauchy product of the seqences an and bn. See Eisenstein series for a discussion of the series and functional identities involved in these formulas.
is called the convolution or the Cauchy product of the seqences an and bn. See Eisenstein series for a discussion of the series and functional identities involved in these formulas.
Since σk(n) (for natural number k) and τ(n) are integers, the above formulas can be used to prove congruences[26] for the functions. See Tau-function for some examples.
Extend the domain of the partition function by setting p(0) = 1.
 [27] This recurrence can be used to compute p(n).
[27] This recurrence can be used to compute p(n).
Let 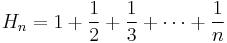 be the nth harmonic number. Then
be the nth harmonic number. Then
 is true for every natural number n if and only if the Riemann hypothesis is true. [28]
is true for every natural number n if and only if the Riemann hypothesis is true. [28]
Miscellaneous
 and
and  where λ(n) is Liouville's function. [29]
where λ(n) is Liouville's function. [29]
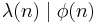 where λ(n) is Carmichael's function. [36] Further,
where λ(n) is Carmichael's function. [36] Further,
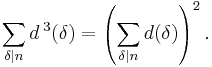 [41] Compare this with 13 + 23 + 33 + ... + n3 = (1 + 2 + 3 + ... + n)2
[41] Compare this with 13 + 23 + 33 + ... + n3 = (1 + 2 + 3 + ... + n)2
 where τ(n) is Ramanujan's function. [44]
where τ(n) is Ramanujan's function. [44]
Notes
- ↑ Hardy & Wright, intro. to Ch. XVI
- ↑ Hardy, Ramanujan, § 10.2
- ↑ Apostol, Modular Functions ..., § 1.15, Ch. 4, and ch. 6
- ↑ Hardy & Wright, §§ 18.1–18.2
- ↑ Hardy & Wright, § 17.6, show how the theory of generating functions can be constructed in a purely formal manner with no attention paid to convergence.
- ↑ Hardy & Wright, Thm. 263
- ↑ Hardy & Wright, Thm. 63
- ↑ Hardy & Wright, Thm. 288–290
- ↑ Hardy & Wright, Thm. 264
- ↑ See Liouville function
- ↑ Hardy & Wright, Thm. 296
- ↑ Hardy & Wright, Thm. 278
- ↑ Hardy & Wright, Thm. 386
- ↑ Hardy, Ramanujan, eqs 9.1.2, 9.1.3
- ↑ Koblitz, Ex. III.5.2
- ↑ 16.0 16.1 Hardy & Wright, § 20.13
- ↑ Hardy, Ramanujan, § 9.7
- ↑ Hardy, Ramanujan, § 9.13
- ↑ Hardy, Ramanujan, § 9.17
- ↑ 20.0 20.1 Ramanujan, On Certain Arithmetical Functions, Table IV; Papers, p. 146
- ↑ 21.0 21.1 Koblitz, ex. III.2.8
- ↑ Koblitz, ex. III.2.3
- ↑ Koblitz, ex. III.2.2
- ↑ Koblitz, ex. III.2.4
- ↑ Apostol, Modular Functions ..., Ex. 6.10
- ↑ Apostol, Modular Functions..., Ch. 6 Ex. 10
- ↑ G.H. Hardy, S. Ramannujan, Asymptotic Formulæ in Combinatory Analysis, § 1.3; in Ramannujan, Papers p. 279
- ↑ See Divisor function.
- ↑ 29.0 29.1 follows from the definitions
- ↑ Hardy & Wright, eq. 22.1.2
- ↑ See prime counting functions.
- ↑ Hardy & Wright, eq. 22.1.1
- ↑ Hardy & Wright, eq. 22.1.3
- ↑ Hardy Ramanujan, eq. 3.10.3
- ↑ Hardy & Wright, § 22.13
- ↑ follows from the definition of λ(n) and Euler's theorem.
- ↑ See Multiplicative group of integers modulo n and Primitive root modulo n.
- ↑ Hardy & Wright, Thm. 329
- ↑ Hardy & Wright, Thms. 271, 272
- ↑ Hardy & Wright, eq. 16.3.1
- ↑ Ramanujan, Some Formulæ in the Analytic Theory of Numbers, eq. (C); Papers p.133
- ↑ Ramanujan, Some Formulæ in the Analytic Theory of Numbers, eq. (F); Papers p.134
- ↑ Apostol, Modular Functions ..., ch. 6 eq. 4
- ↑ Apostol, Modular Functions ..., ch. 6 eq. 3
References
- Tom M. Apostol (1976), Introduction to Analytic Number Theory, Springer Undergraduate Texts in Mathematics, ISBN 0387901639
- Apostol, Tom M. (1989), Modular Functions and Dirichlet Series in Number Theory (2nd Edition), New York: Springer, ISBN 0-387-97127
- Hardy, G. H. (1999), Ramanujan: Twelve Lectures on Subjects Suggested by his Life and work, Providence RI: AMS / Chelsea, ISBN 978-0821820230
- Hardy, G. H.; Wright, E. M. (1980), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0198531715
- G. J. O. Jameson (2003), The Prime Number Theorem, Cambridge University Press, ISBN 0-521-89110-8
- Koblitz, Neal (1984), Introduction to Elliptic Curves and Modular Forms, New York: Springer, ISBN 0-387-97966-2
- William J. LeVeque (1996), Fundamentals of Number Theory, Courier Dover Publications, ISBN 0486689069
- Elliott Mendelson (1987), Introduction to Mathematical Logic, CRC Press, ISBN 0412808307
- Ramanujan, Srinivasa (2000), Collected Papers, Providence RI: AMS / Chelsea, ISBN 978-0821820766
External links
- Elementary Evaluation of Certain Convolution Sums Involving Divisor Functions PDF of a paper by Huard, Ou, Spearman, and Williams. Contains elementary (i.e. not relying on the theory of modular forms) proofs of divisor sum convolutions, formulas for the number of ways of representing a number as a sum of triangular numbers, and related results.
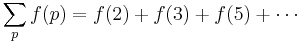
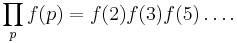
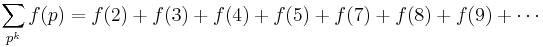


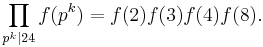

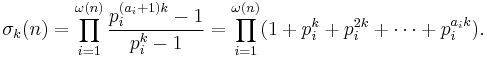
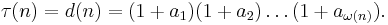
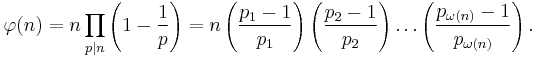
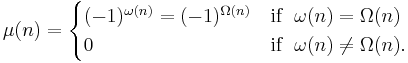
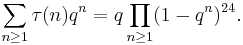
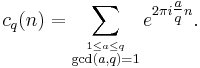

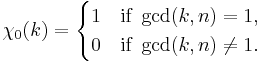



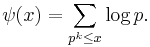



![\lambda(p_1^{a_1}p_2^{a_2} \dots p_{\omega(n)}^{a_{\omega(n)}}) = \operatorname{lcm}[\lambda(p_1^{a_1}),\;\lambda(p_2^{a_2}),\dots,\lambda(p_{\omega(n)}^{a_{\omega(n)}}) ].](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/a4abc3567c1fc7c3f13b28be556eaaf5.png)
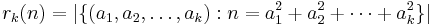
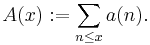

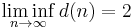

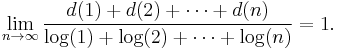


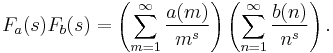

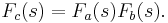

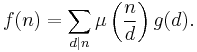

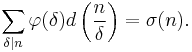
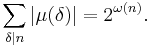


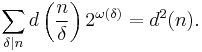

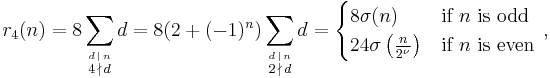 where ν = ν2(n).
where ν = ν2(n). 
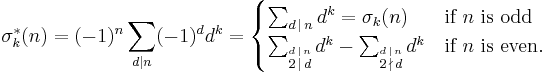
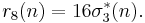
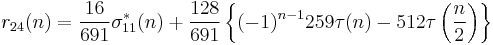
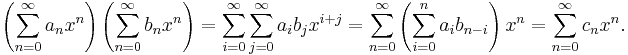

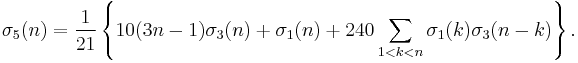


 where τ(n) is Ramanujan's function.
where τ(n) is Ramanujan's function. 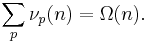

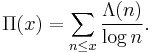

![e^{\psi(x)}= \operatorname{lcm}[1,2,\dots,\lfloor x\rfloor].\;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4d597311fe4ecc0ba228a0a85cdecacf.png)